 Thermodynamics is the study of the movement of heat and its relationship with work. Throughout this topic of thermodynamics, we need to agree on a few key terms.
Thermodynamics is the study of the movement of heat and its relationship with work. Throughout this topic of thermodynamics, we need to agree on a few key terms.
Key Concepts
Thermal energy is an energy store in a body of matter. Zoom in far enough, and thermal energy becomes the sum of the kinetic energy of the individual particles.
Heat is an energy pathway, a mechanism by which energy can be transferred from one body to another.
Work is the product of the force exerted by a body and the distance travelled parallel to the force.

We will refer to three types of system:
| System type | Heat can pass in and out? | Work can be done? | Matter exchange with surroundings? | Example |
|---|---|---|---|---|
| Open | 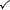 | 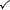 | 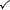 | Kettle with spout |
| Closed | 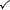 | 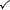 | 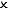 | Gas syringe |
| Isolated | 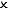 | 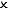 |  | Perfect vacuum flask (or the universe!) |
The first law of thermodynamics combines changes in temperature and work done. It is a restatement of conservation of energy:
The amount of heat that enters a closed gas container is equal to the sum of the increase in internal energy and the work done by the gas on the surroundings.
\(Q=\Delta U+W\)
- \(Q\) is heat (J), with \(Q> 0\) for heat entering the gas container
- \(\Delta U\) is change in internal energy (J), with \(\Delta U >0\) for an increase in the internal energy of the gas
- \(W\) is work done (J), with \(W>0\) for work done on the surroundings by the gas
There is a logical flow to the equation when expressed with respect to \(Q\).

 Video Solution
Video Solution Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn