Radioactive decay is a random process. This leads to an interesting link with mathematics.
If the rate of change of a quantity is proportional to the quantity itself then the change is exponential.
Key Concepts
Nuclear decay is a random process. In a sample of unstable nuclei:
- We do not know which nucleus will be the next to decay
- We do not know when the next nucleus will decay
- There is a fixed probability that a given proportion of decays will occur in a given period of time. For a large sample of dice, one sixth would land on a six in a given roll.
The probability of decay is related to the amount of energy that will be released when it happens.
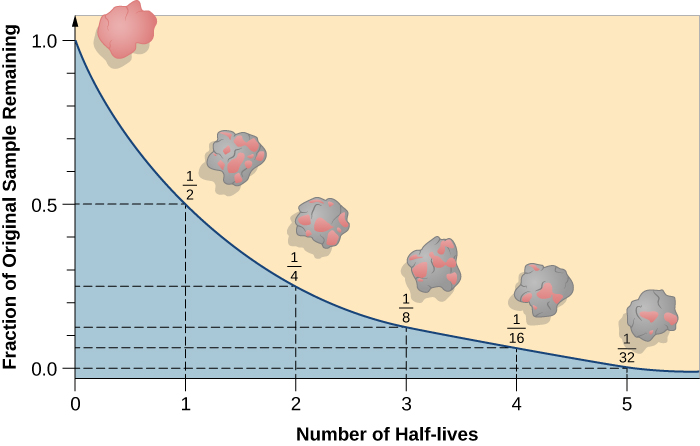
The consequence of the random nature of decay can be demonstrated with a more everyday substance: beer foam. Since the bubbles pop randomly, the amount of beer foam in a glass decays exponentially.
Exponential decay graphs are an example of a Non-linear graph.
Half life gives a measure of the rate of decay of a sample. Protactinium is an isotope with a half life of about 1 minute. This makes it convenient for school experiments.
There are methods for measuring short and long half lives:
- If the half life is short, a Geiger-Muller tube and counter can collect measurements for how count rate varies with time. The background count rate must be measured (without the presence of the sample) and deducted from each reading. A graph can be plotted of count rate against time, and the half life measured and confirmed using intervals on the count axis.
- The activity of isotopes with half lives of hundreds or thousands of years does not noticeably decrease in the time over which observations can be made. Instead, to find half life, a pure sample of the isotope can be isolated. The mass can be used to find the number of nuclei, which is combined with the activity to find decay constant.
Half life is often the quantity that is quoted for a given isotope in exam questions. A good tip for commencing further calculations is to use the half life to find the decay constant:
\(\lambda={\ln2\over t_{1\over 2}}\)
- \(\lambda\) is the decay constant
- \(t_{1\over2}\) is the half life
The half life of a isotope can be used to determine whether the isotope may have uses for mankind:
- The long half life of carbon-14 (5730 years) means it can be used to date ancient objects
- The short half life of technetium-99m (6 hours) permits the medical use as a tracer in the human body
Exponential decay
If \({\mathrm{d} N\over \mathrm{d}t} ∝ N\) then the decay is exponential:
\(N =N_0\mathrm{e}^{-\lambda t}\)
- \(N\) is the number of undecayed nuclei remaining
- \(N_0\) is the number of undecayed nuclei when \(t=0\)
- \(\lambda\) is the decay constant, a fixed probability of a given proportion of nuclei decaying per unit time (units correspond to \(t\) e.g. s-1)
- \(t\) is time (e.g. s)
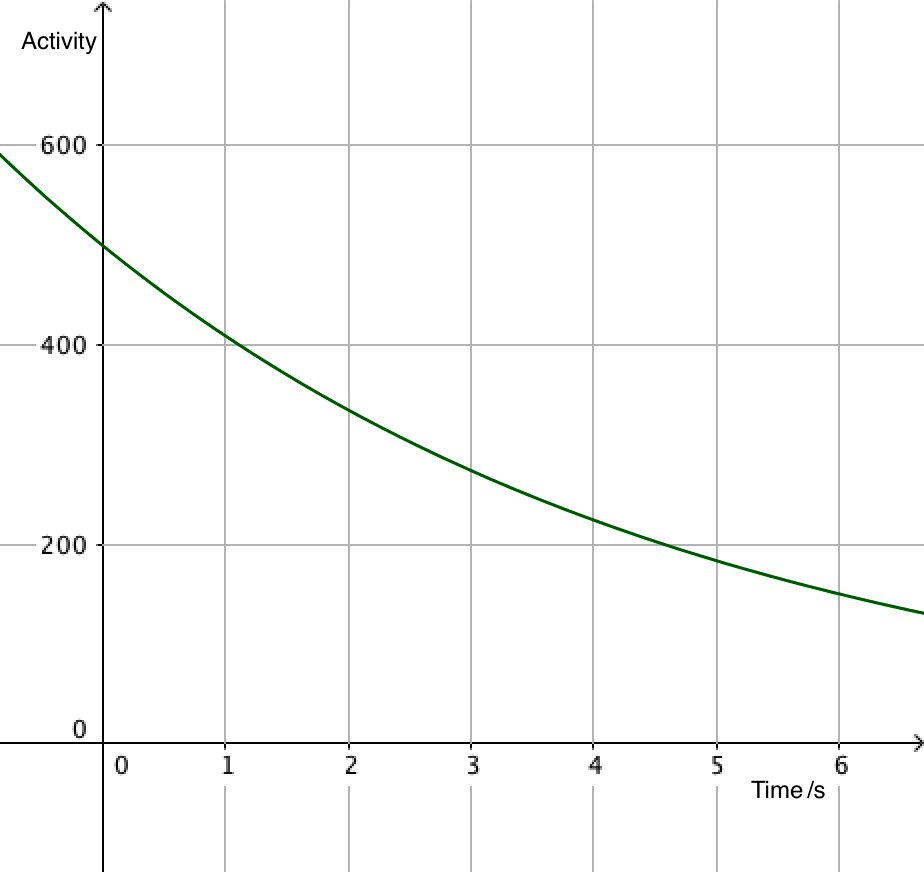
Since activity is proportional to the number of undecayed nuclei, it is also exponential, leading to equations that can often be more useful than the number of particles. After all, it's difficult to count individual nuclei!
\(A=\lambda N_0\mathrm{e}^{-\lambda t}\)
\(A =A_0\mathrm{e}^{-\lambda t}\)
- \(A\) is the activity of the source (s-1)
- \(A_0\) is the activity when \(t=0\)
The exponential decay equation enables the calculation of the number of nuclei remaining at any time.
A linear relationship can be produced by taking natural logarithms of each side of the equation:
\(\ln A=-\lambda t+\ln{A_0}\)
This is the kind of mathematical manipulation that may required for your Investigation.
Use flashcards to practise your recall.
Use quizzes to practise application of theory.
START QUIZ!
The diagram shows 4 lines
Which one is exponential?
The others are 1/x, 1/x2 and a parabola
The blue line below has the equation y = e-x
The equation of the red line is:
points on the blue line are simply multiplied by 3
Radioactive decay is exponential because:
the gradient of an exponential curve is proportional to the x value
The graph shows activity vs time for a given isotope
The half life is
time to decay to 250
The graph shows the activity vs time for a given isotope
If the initial activity (for the same isotope) had been 400 Bq how long would it take for the activity to reach 100 Bq
The half life is 2 s it doesn't matter that there is a lower starting point
400 to 100 is two half lives
Some radioactive isotopes are used in medicine. They are injected into the blood and enable different organs to show up on scanners.
A suitable half life for such an application would be:
Needs to be radioactive for long enough to use but not so that the body is radioactive for a long time afterwards
Protactinium is an example of an isotope used to measure half life in school labs.
An isotope used for this experiment could have a half life of
with a half life of 5 mins there will be a measurable decrease in activity during a lesson
Which combination of activity and half life would be best for an alpha emitter suitable for use in the school lab.
Needs to have a measurable activity but not decay too quickly. 100 MBq would be too radioactive for school use.
The equation for exponential decay is
N = Noe-λt
where λ is the decay constant.
The unit for λ is
λt must be a number without units so if λ has units s-1 then λt will have units s/s ⇨ no units
An isotope has a decay constant 0.1 s-1. If its original activity is 1 MBq what will its activity be after 10 s
A = Aoe-λt
Substitute into the equation
Twitter 
Facebook 
LinkedIn