Pre-IB Weekly Quiz 4

  2. Pre-IB Preparation
  3. Pre-IB Weekly Quiz 4
    4. 30'

This page contains your fourth weekly quiz! Each week of July and August a new quiz will be published, so that you can make sure you are ready to start the Maths AI course in September with confidence.  

1

If \(4g+5=40-3g\), what is the value of \(g\)? (to 3sf)

g=

1.Add 3g to both sides

2. Subtract 5 from both sides

3. Divide both sides by 7

2

What is the longest length of a triangle with shorter sides 3 and 4?

Use Pythagoras to calculate this:

\(\sqrt{\left(4^{2}+3^{2}\right)}\)

3

Rearrange the equation \(y=0.5x+4\) to make \(x\) the subject

x=

1. Subtract 4 from boths ides.

2. Divide both sides by 0.5, which is equivalent to multiplying both sides by 2.

4

Consider the linear model, f(x) = 3.42x -1.7, what is the value of x when f(x) = 49.6?

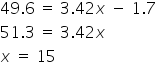49.6 space equals space 3.42 x space minus space 1.751.3 space equals space 3.42 xx space equals space 15 or input y = 342x - 1.7 in to your GDC and read from the table.

5

Consider the linear function 5x - 2y - 8 = 0. It crosses the y - axis at the point (0,-4), what is its gradient?

Rearrange to get 2y = 5x - 8 and then divide by 2 to get y = 2.5x - 4

6

Find the equation of the line with gradient 15 that passes through (3,35), written in the form \(y=mx+c\)

y=

1. Substitute the gradient and a coordinate into the equation of a straight line formula

(for more support with this specific skill, watch video 6 in the 'pre-IB preparation' page)

7

Simplify

\({ { (2 }^{ 3 }) }^{ 4 }\)

This is equivalent to \({ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } \times{ { 2 }^{ 3 } } \times { { 2 }^{ 3 } } .\) As the bases are the same we can now simply add together the exponents.

8

Which formulae below find the circumference of a circle, C, with radius, r, and diameter, d?

See answers.

9

A semi-circlular logo has a radius of 10cm. Find the area of the logo, giving your answer to 1 decimal place.

We could use the formula for the area of a sector, with the angle, \(\theta\), being 180 degrees. However, it may be more efficient to use the formula for the area of a circle and then divide that area by 2 to get the area of the semi-circle.

\(A=\frac { \pi \times { 10 }^{ 2 } }{ 2 } =157.0796{ cm }^{ 2 }=157.1{ cm }^{ 2 }\)

10

Find the volume of the cylinder with diameter 10cm and height of 10cm. Give your answer in terms of pi.

Volume= \(\pi cm^3\)

\(\pi\cdot5^{2}\cdot10\)