 Go from exam failure to exam ace. Improve your predicted grade from a 3 to a 7. Become an expert at IBDP mathematics. It would be nice if, by following a few tips on an 'exam tips' page, we could all magically achieve that overnight. The truth is that improvement in mathematics is gradual, it takes effort, good study skills and the right advice. However, there are a lot of little things that you can do in your preparation for an examination to ensure that you do the best you possibly can. Sports coaches often look at marginal gains that make tiny 1% improvements. This page aims to help you make those tiny improvements that could add up to something significant and ensure that you avoid a few errors of judgment that could lead to failure.
Go from exam failure to exam ace. Improve your predicted grade from a 3 to a 7. Become an expert at IBDP mathematics. It would be nice if, by following a few tips on an 'exam tips' page, we could all magically achieve that overnight. The truth is that improvement in mathematics is gradual, it takes effort, good study skills and the right advice. However, there are a lot of little things that you can do in your preparation for an examination to ensure that you do the best you possibly can. Sports coaches often look at marginal gains that make tiny 1% improvements. This page aims to help you make those tiny improvements that could add up to something significant and ensure that you avoid a few errors of judgment that could lead to failure.
Memorize key Facts
Trigonometry Exact Values
You definitely need to know these before paper 1.
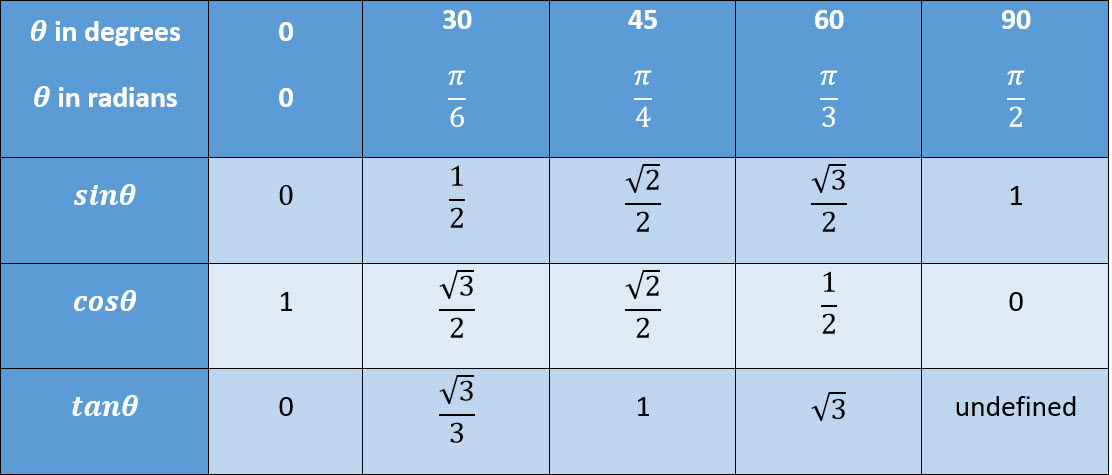
Graphs of Sine Cosine and Tangent Functions
Ensure that you know how to sketch these graphs so that you can work out the key properties of the functions
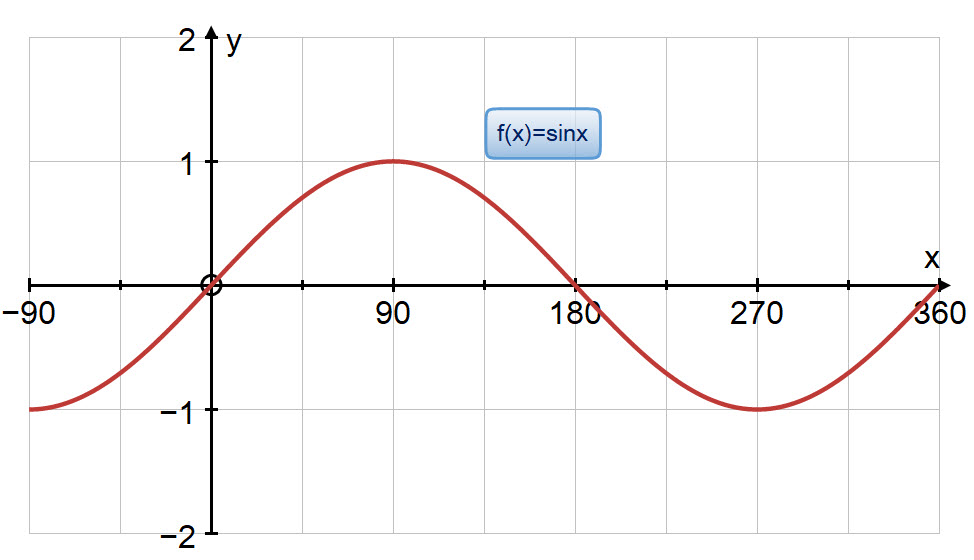
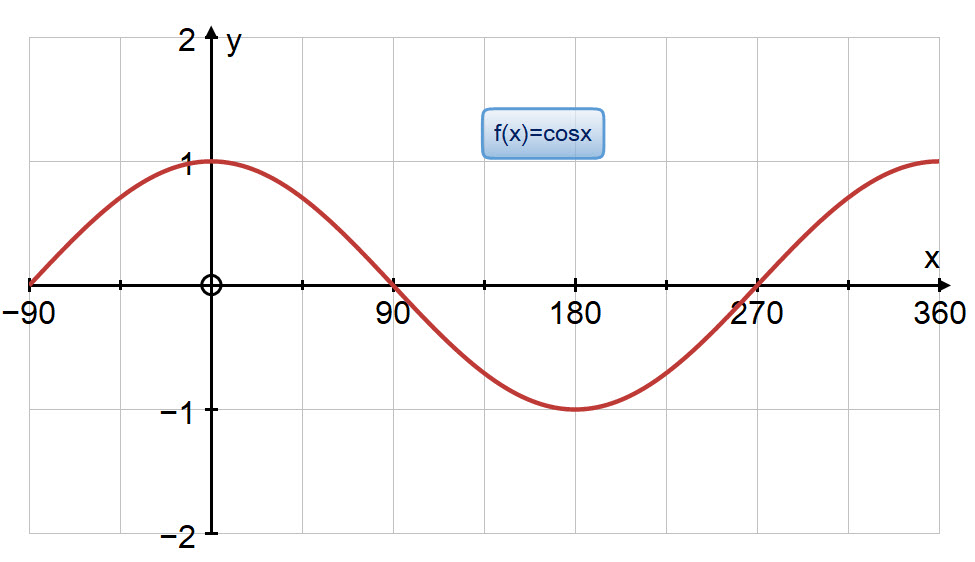
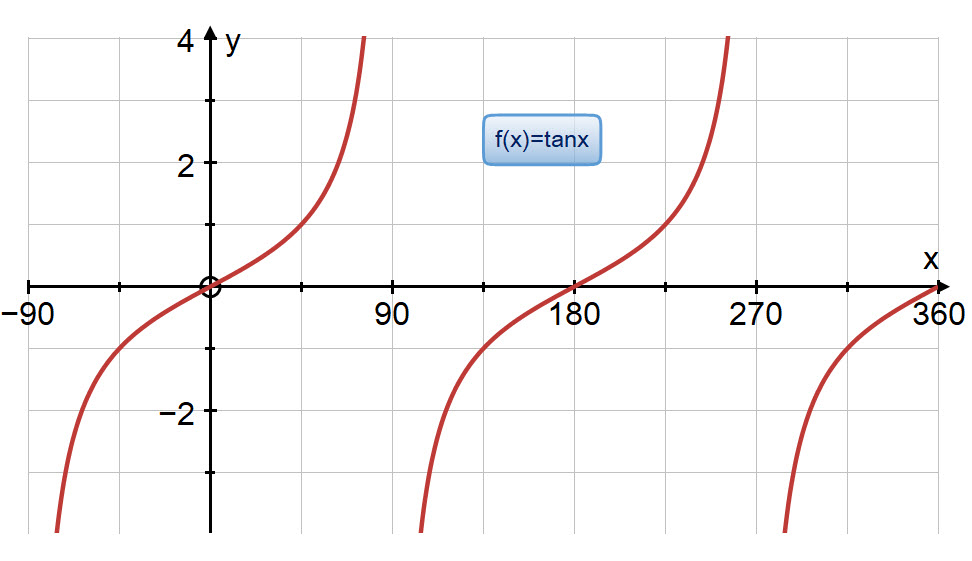
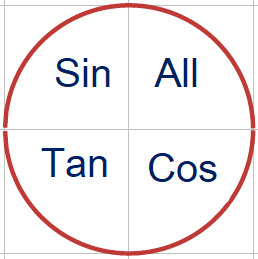
Some students like to use the following diagram to remind them in which quadrants each of the trigonometric ratios is positive
Chain Rule
You should know how to use the Chain Rule to differentiate a composite function, but you are sometimes required to know the general form when the question is given in function notation. This is not in the formula booklet
\(h(x)=f[g(x)]\\ h'(x)=g'(x)f'[g(x)]\)
This is useful for answering exam questions like the following
Consider two functions f and g and their derivatives f' and g'. The following table shows the values for the two functions and their derivatives at x = -1, 0, 1
| -1 | 0 | 1 | |
|---|---|---|---|
| f(x) | -2 | 1 | 6 |
| g(x) | 3 | -1 | 1.5 |
| f'(x) | 2 | 3 | 4 |
| g'(x) | 4 | -2 | 3 |
\(h(x) = f\circ g(x)\)
Find h'(0)
Answer = -2
h'(x) = g'(x)f'(g(x))
h'(0) = g'(0)f'(g(0))
h'(0) = g'(0)f'(-1)
h'(0) = -1\(\times\)2
h'(0) = -2
There are other formula that are derived from the Chain Rule. It helps your speed if you can memorize these
Need some practice in using these? Why not try a quiz from Chain Rule page
Integration by Recognition
These integrals can all be found by integration by substitution, but if you can recognize them, you can save yourself a lot of time
 Properties of Vector Product
Properties of Vector Product
There are several properties of the vector product that do not appear in the formula booklet
 Properties of Complex Numbers
Properties of Complex Numbers
There are several properties of complex numbers that do not appear in the formula booklet
text
 In the examinations, you are given 5 minutes reading time. Many students don't like, nor make good use of, this time. Quickly glancing at unfamiliar questions can cause panic. Don't forget that this 5 minutes is a bonus, so make the most of it! You are not allowed to write anything down during this time, but it is useful for helping you organise yourself, gather your thoughts and decide on a plan for the examination that follows. In your revision, you should practise papers under timed conditions and include this reading time to decide how best to use it. Here are some suggestions as to how you might use it
In the examinations, you are given 5 minutes reading time. Many students don't like, nor make good use of, this time. Quickly glancing at unfamiliar questions can cause panic. Don't forget that this 5 minutes is a bonus, so make the most of it! You are not allowed to write anything down during this time, but it is useful for helping you organise yourself, gather your thoughts and decide on a plan for the examination that follows. In your revision, you should practise papers under timed conditions and include this reading time to decide how best to use it. Here are some suggestions as to how you might use it- Quickly glance through the paper and check that you there are not any missing questions or pages. This should also enable you to not miss out any questions and avoid that OMG, I didn't see that last page!
- Find some questions that you like the look of and start thinking about how you might start them.
- There will be some unfamiliar questions. Try not to panic. Once you have got warmed up, you will be in a better position to try them.
- Take a few deep breaths.
 The examination is divided into two sections: section A (write on the paper), section B (write in the booklet). The marks available for the two sections are approximately equal, so you should divide your time equally between them. Many students spend too long on section A and run out of time on section B. The questions in section A gradually increase in difficulty and the last question in section A is for superhuman students who are aiming at a high grade 7. Do not spend too much time on this question and be prepared to leave it out (you can always come back to it at the end). Which would you rather do: the last question in section A worth 6-8 marks or the last question in section B worth 18-24 marks?
The examination is divided into two sections: section A (write on the paper), section B (write in the booklet). The marks available for the two sections are approximately equal, so you should divide your time equally between them. Many students spend too long on section A and run out of time on section B. The questions in section A gradually increase in difficulty and the last question in section A is for superhuman students who are aiming at a high grade 7. Do not spend too much time on this question and be prepared to leave it out (you can always come back to it at the end). Which would you rather do: the last question in section A worth 6-8 marks or the last question in section B worth 18-24 marks?
text
Show that vs Verify
The term show that comes up in long section B questions, it is there to help you. First of all, you know the answer that you are trying to attain and secondly, if you are unable to get the answer, you can carry on with the next part using the answer given in the question. In questions that require you to show that you must try to avoid working backwards from the answer.
A question that asks you to verify requires only for you to provide evidence that validates a result, perhaps by substituting a value into a formula.
Here are two examples that should help you to see what to do:
Example 1
Point A (-2 , k) lies on the line r = \(\left( \begin{matrix} 1 \\ 2 \end{matrix} \right) +s\left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \)
Show that k = 11
Here you must avoid working backwards from the answer of 11 to verify that A lies on the line.
Start with the idea that A lies on the line and find the value of s
\(\left( \begin{matrix} -2 \\ k \end{matrix} \right) =\left( \begin{matrix} 1 \\ 2 \end{matrix} \right) +s\left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \)
-2 = 1 - s
s = 3
Now find k
k = 2 + sx3
k = 2 + 3x3
k = 11
Example 2
Let f(x) = ax² + 12x + c.
A horizontal line intersects with the graph of f at x = -2 and x = 6.
a) Find the equation of the axis of symmetry
b) Hence, show that a = -3
a) the axis of symmetry lies halfway in between x = -2 and x = 6
\(\frac{-2+6}{2}=2\)
axis of symmetry is x = 2
b) We should not substitute the value of a into the function and verify that the line of symmetry is x = 2, we should start with the fact that we know that the axis of symmetry is x = 2 - the word hence helps us to see that this part follows on from what we know in part a).
For the general quadratic function, f(x) = ax² + bx + c, the equation of the axis of symmetry is x = \(\frac{-b}{2a}\)
For our function, f(x) = ax² + 12x + c, the equation of the axis of symmetry is x = \(\frac{-12}{2a}\)
Hence \(\frac{-12}{2a}=2\)
-6 = 2a
a = -3
Sketch vs Plot
In questions that ask you to sketch, you are not expected to draw an accurate plot of a graph using graph paper. You need to include key information: local maxima/minima, intercepts and equations of asymptotes.
In questions asking you to plot, you are often required to mark the position of points on a diagram.
Here is an example to show you what might be expected in a question asking you to sketch a graph of a function:
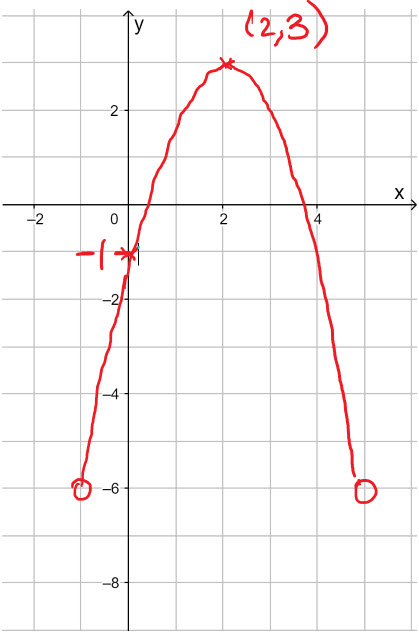
Let f(x) = -(x - 2) + 3
a) Write down the vertex of the graph of f
b) Sketch the graph of the f for \(-1\le x\le 5\) on the grid below
a) Vertex at (2 , 3)
b) We could be expected to include the vertex, the y intercept and the end points of the function
Hence
The word hence is there to help you. You should be using something that you found in the previous part to help you find the answer to this question. If you ignore this, not only do you risk wasting time, but also marks, since using a different method may get you no marks!
Here is an example:
The first three terms of a geometric sequence are 4m + 5 , 10 , m - 1
a) Write down an expression for the common ratio, r
b) Hence, show that 4m² + m - 105 = 0
a) Since this is a geometric sequence, the ratio can be found by dividing the 2nd term by the 1st term
\(r = \frac{10}{4m+5}\)
b) The hence tells us we need to use the result from part a).
Let's use the same method. The ratio can be found from dividing the 3rd term by the 2nd term
\(r = \frac{m-1}{10}\)
Hence, \(\frac{10}{4m+5}=\frac{m-1}{10}\)
100 = (4m+5)(m-1)
100 = 4m² + m - 5
0 = 4m² + m - 105
This question also includes the command term show that. What we cannot do here is use the quadratic equation to find m (m =\(\frac{-21}{4}\) , m = 5) and substitute this into the expressions and verify that we have three terms of a geometric sequence.
Hence or otherwise
This is very much like hence, but is meant more for guidance. The previous part of a question may guide you to use a particular method, this may be the quickest and most obvious method. However, you will not be penalised if you use an alternative method.
Write down
This means you probably won't have to do any working out (or not much at least). You should be able to complete this fairly quickly.
text
On paper two, you risk losing several marks if you do not round your answers appropriately. According to the reports by examiners, some students don't seem to know the difference between rounding to 3 decimal places and rounding to 3 significant figures. This is an easy one to get right!
Here's a recap of significant figures if you need it:
- Significant figures are a way of rounding numbers that allow you to always be consistent in the accuracy of your answers.
- The first significant figure is the first non-zero digit.
- Start counting significant figures after this digit.
- Any zeros between non-zero digits are significant.
- Stop counting (for 3 sig figs) when you get to the third significant figure
- Decide to round up or down
Example 1
0.00305
The 1st significant figure is 3
The 2nd significant figure is 0 (the zero between 3 and 5 is SIGNIFICANT)
The 3rd significant figure is 5
Example 2
Round the following numbers to 3 significant figures
a) 82 761 \(\approx \) 82 800
b) 0.001358 \(\approx \)0.00136
c) 57.0098 \(\approx \) 57.0
 Ready for a quick Quiz?
Ready for a quick Quiz?
START QUIZ!
Significant Figures 1/1
Round the following numbers to 3 significant figures
5.11405 \(\approx \)
Round the following numbers to 3 significant figures
7074.75 \(\approx \)
Round the following numbers to 3 significant figures
0.003056 \(\approx \)
Round the following numbers to 3 significant figures
100059 \(\approx \)
Round the following numbers to 3 significant figures
38999 \(\approx \)
text
- Make sure that your calculator has the latest operating system/firmware and you know how to put it in examination mode (press to test). You should practise using it in this mode to avoid any surprises.
- Students often use an analytical method and waste time when they should use their calculators. Once an equation is set up, use your calculator to solve it.
- Several marks for a question suggests working out needs to be shown.
- Sketch the output of graphing screen to show key features which lead to answer. Don't forget to label axes.
- Round only at end of the question, that is, use more than 3 significant figures in calculations. Better still, know how to use calculator memory.
text
- Read the questions carefully. Underline key terms. This will slow you down and allow you to think and may give you a clue as to how to solve the problem.
- Write down as much information as you can. In the question below, you are given credit for recognising that it is a question about binomial probabilities. Write down all your thinking!

- Draw diagrams and graphs to help you visualize the problem:

 The formula booklet is your friend. Get to know it. Get your own copy and be familiar with the contents. Annotate it and don't waste any time learning any of the formula that are given in it.
The formula booklet is your friend. Get to know it. Get your own copy and be familiar with the contents. Annotate it and don't waste any time learning any of the formula that are given in it.- Scrap for marks. If you cannot do part b, then maybe you can do part c. It is not necessarily more difficult. Make use of 'show that' questions to carry on when you get stuck.
- Check your answers. If you have time at the end of the exam go through the paper and check, check, check! Errors are often hard to find. Look for any results that seem strange.
- Don't cross out any of your working out (unless you are replacing it with something else). You probably have some working or thinking that is correct and that you will be given credit for.
 Predict questions on paper 2. Straight after paper 1, get together with your friends and make a list of the topics that were on it. Any topics that were not covered in paper 1 are likely to be tested on paper 2. This will help you decide what to concentrate on the evening before paper 2. Remember, you are NOT ALLOWED to discuss the exam outside your school community.
Predict questions on paper 2. Straight after paper 1, get together with your friends and make a list of the topics that were on it. Any topics that were not covered in paper 1 are likely to be tested on paper 2. This will help you decide what to concentrate on the evening before paper 2. Remember, you are NOT ALLOWED to discuss the exam outside your school community.- Try to get a good night's sleep before the exam. You need to be fresh and 1 more hour of sleep might be better than 1 more hour of revision.
text
Feedback
Which of the following best describes your feedback?
Notes
Report a problem for flashcard
Your best time:

 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn